Bu yazıda küçük partilere desteğin ölçülmesinin neden zor olduğunu açıklayacağım. Küçük partiler özelinde hazırladığım inceleme, başka düşük yüzdeli grupların (örneğin dini azınlıklar) ölçümünün zorluğu için de geçerlidir.
Yakın geçmişte bir seçim olmadığı sürece, A partisinin gerçek oy oranını tespit edemeyiz. Ancak, örneğin anlaşılması için, A partisinin gerçek oy oranının %1 olduğunu varsayalım. Anketler vasıtasıyla A partisinin oy oranını hesaplayabiliriz. Bin farklı anketin basit rastsal örneklem metoduyla A partisinin oy oranını ölçtüğünü farz edelim. Bunu örneklem dağılımı (sampling distribution) için R Studio üzerinden simülasyon yaparak gösterebiliriz. Benim yaptığım simülasyonda dağılım şu şekilde çıktı:
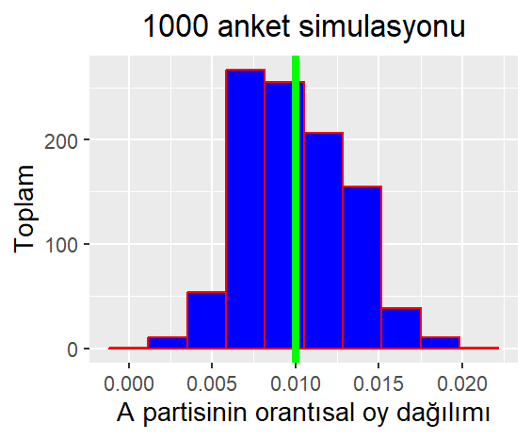
Figür 1’deki simülasyonda gördüğümüz üzere, anketler point estimate (nokta hesaplama) konusunda göreceli olarak başarılı çıktı. Anketlerin %84’ünde A partisinin oy oranını hesaplamaları %.05’in üstünde ve %1.5’in altındaydı. Dağılımın en yaygın olduğu kutu, .01 değerine (%1, yeşil çizgi) çok yakın.
Reel hayattaysa bu egzersizde karşılaşmadığımız bir sorun var. O da A partisinin gerçek oy oranını bilmememiz. Yani Figür 1’de gördüğümüz yeşil çizgi aslında meçhuldür. Bu durumda A partisinin oy oranını belirli güven aralığı dahilinde hesaplayabiliriz. Güven aralığı, Figür 1’deki gibi çokça örneklem çekildiğinde, A partisinin olası oy oranını için belirli alt ve üst limit tahminleri sunar. Güven aralığı belirlerken önceden bir güven seviyesi (%90, %95…) seçilir. Formülse aşağıdaki şekildedir:
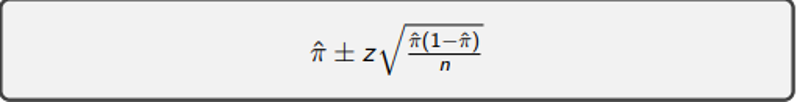
Figür 2’deki şapkalı pi, anketten hesapladığımız A partisinin oy oranıdır. Z-skoru, güven aralığı için örneklem dağılımında kabul edeceğimiz standart sapma miktarıdır. %95 güven aralığı için kullanacağımız standart sapma 1.96’dır. Karekök içerisindeki hesaplama ise standart hatadır. Anketimizin A partisinin oy oranını %100 doğrulukla tahmin ettiğini varsayalım. Bu durumda şapkalı pi değerimiz .01 olacaktır. Standart hata ise 
üzerinden .003 olarak hesaplanır. Yani standart hata, nokta hesabımızın (.01) yaklaşık %30’u kadardır ki bu büyük bir rakamdır. Bunun sebebiyse bölendeki .01 ile .99’ın çarpımının karekökünün göreceli olarak yüksek bir değer olmasıdır (.01). Şapkalı pi, .5’e yaklaştıkça bu değer düşecektir.
Kural: Düşük oranlarda standart hatanın nokta hesabına göreceli oranı yüksektir. Oran .5’e yaklaştıkça standart hatanın göreceli değeri düşerken gerçek (absolute) değeriyse artar.
Göreceli oranın yüksekliği, A partisinin oy oranını tespitte işimizi zorlaştırır. Bunu bir simülasyon üzerinden anlayabiliriz. Figür 1’deki simülasyonumuzu tekrarlayalım. Ancak bu sefer nokta hesaplarımızın dağılımı yerine güven aralıklarımızın dağılımını gösterelim. Tekrarlamak gerekirse, güven aralığı hesaplarken, z-değerini standart sapma ile çarpar, elde ettiğimiz sayıyı nokta hesabımıza ekler ve nokta hesabımızdan çıkartırız (Figür 2).
Figür 3’teki güven aralığında baktığımızda ise Figür 1’e nazaran belirsizliğin arttığını görürüz. Örneğin Figür 3’te 702 ankette güven aralığı A partisinin oy oranının %0.05’in altında olabileceğini belirtir. 537 hesaplamaya göreyse A partisinin oy oranı %1.5’in üzerinde olabilir. Hakeza 206 hesaplamada, A partisinin oy oranı %2’nin üzerinde olabilir. Güven aralığı hesaplamaları, Figür 1’deki örneklem dağılımına nazaran daha ekstrem değerleri daha sık kapsar. Bu da A partisinin oy oranını belirlememizi zorlaştırır.
Sonuç
Rastsal örneklerle yapılmış anketler, küçük partilerin (veya düşük yüzdeli grupların) oy oranlarının nokta atışını (point estimate) genellikle doğru tespit eder. Ancak, buna rağmen anketler üzerinden A partisinin oy oranına yüksek güvenle çıkarım yapabilmek zordur. Yani, anketin %2 gösterdiği bir partinin gerçek oy oranının %2, hatta %0 çıkma olasılığı yabana atılmayacak düzeyedir. Bu durumun nedeni de düşük yüzdeli gruplarda, standart hatanın nokta hesabına oranının yüksek olmasıdır. Küçük partilerin toplumsal desteğini ölçmede, anketlere ek olarak, alternatif yollara (örneğin partilerin yerelde örgütlenme seviyesi) bakılması, oy oranlarını doğru tespit etmede yardımcı olabilir.